From Static to Numeric to Single-Choice Exercises in R/exams
Idea
Our colleagues over at the economics department became interested in using R/exams for
generating large-scale exams in their introductory economics courses. However, they face the challenge that
so far they had been writing static exercises and modified them by hand if they wanted to reuse them in a
different exam in another semester. To let R/exams do this job it is illustrated how a static arithmetic
exercise can be turned into a dynamic exercise template either in num
format with a numeric solution or into schoice format with a single-choice solution.
The idea for the exercise is a very basic price elasticity of demand task:
| Consider the following inverse demand function: for the price given the demanded quantity . What is the price elastiticy of demand at a price of ? |
The natural candidates for “parameterizing” this exercise are the price and the parameters and of the inverse demand function. Based on these the solution is simply:
| First, we obtain the demand function by inverting the inverse demand function: . Then, at the price elasticity of demand is |
Overview
Below various incarnations of this exercise are provided in both R/Markdown Rmd and R/LaTeX Rnw format.
The following table gives a brief overview of all available versions along with a short description of the idea behind it.
More detailed explanations are provided in the subsequent sections.
| # | Exercise templates | Dynamic? | Type | Description |
|---|---|---|---|---|
| 1 | elasticity1.Rmd elasticity1.Rnw |
No | num |
Fixed parameters and numeric solution. |
| 2 | elasticity2.Rmd elasticity2.Rnw |
No | schoice |
As in #1 but with single-choice solution (five answer alternatives). |
| 3 | elasticity3.Rmd elasticity3.Rnw |
Yes | num |
Randomly drawn parameters with dynamic computation of correct solution, based on #1. |
| 4 | elasticity4.Rmd elasticity4.Rnw |
Yes | schoice |
Randomly drawn parameters (as in #3) with dynamically-generated single-choice solution (as in #2), computed by num_to_schoice(). |
| 5 | elasticity5.Rmd elasticity5.Rnw |
Yes | schoice |
As in #4 but with the last alternative: None of the above. |
Static numeric
The starting point is a completely static exercise as it had been used in a previous introductory economics exam. The parameters had been set to , , and . This implies that , leading to an elasticity of .
The corresponding R/exams templates simply hard-code these numbers into the question/solution and wrap everything into R/Markdown (elasticity1.Rmd) or R/LaTeX (elasticity1.Rnw). Note that LaTeX is used in either case for the mathematical notation. In case you are unfamiliar with the R/exams format, please check out the First Steps tutorial.
The meta-information simply sets extype to num, supplies the exsolution with a precision of three digits,
and allows an extol tolerance of 0.01. To see what the result looks like download the files linked above
and run exams2html() and/or exams2pdf(). (The examples below always use the R/Markdown version but the
R/LaTeX version can be used in exactly the same way.)
library("exams")
exams2html("elasticity1.Rmd")
exams2pdf("elasticity1.Rmd")
Static single-choice
Single-choice versions of exercises are often desired for use in written exams because they can be conveniently scanned and automatically evaluated. Thus, we need to come up with a number of incorrect alternative solutions (or “distractors”). If desired, these could include typical wrong solutions or a None of the others alternative.
The R/exams templates elasticity2.Rmd and elasticity2.Rnw are essentially copies of the static numeric exercise above but:
- Question/solution now contain an answerlist (with five alternatives).
- The
extypehas been changed toschoice. - The
exsolutionnow contains a binary coding of the correct solution. - Furthermore, to obtain some basic randomization we have turned on shuffling by setting
exshuffletoTRUE. (Subsampling more than five alternatives would also be possible and would add some further randomization.)
As above exams2html() and/or exams2pdf() can be used to display the exercise interactively in R/exams.
Dynamic numeric
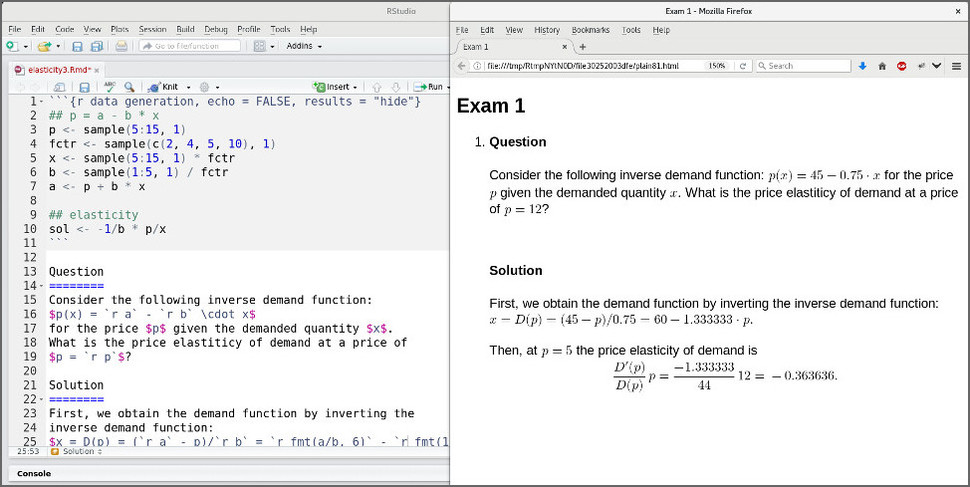
Next, the static exercise from above is made dynamic by drawing the parameters from a suitable data-generating process. In this case, the following works well:
## p = a - b * x p <- sample(5:15, 1) fctr <- sample(c(2, 4, 5, 10), 1) x <- sample(5:15, 1) * fctr b <- sample(1:5, 1) / fctr a <- p + b * x ## elasticity sol <- -1/b * p/x
Note that in order to obtain “nice” numbers a common scaling factor fctr is used for both x and b.
Also, while the examinees are presented with parameters a and b and have to compute x,
the data-generating process actually draws x and b and computes a from that. Again, this makes it
easier to obtain “nice” numbers.
The R/exams templates
elasticity3.Rmd and
elasticity3.Rnw include
the data-generating process above as a code chunk either in R/Markdown or R/LaTeX format.
The parameters are then inserted into question/solution/metainformation using `r a` (R/Markdown)
or \Sexpr{a} (R/LaTeX). Sometimes the fmt() function is used for formatting the parameters
with a desired number of digits. (See ?fmt for more details.)
As before exams2html() and/or exams2pdf() can be used to display the random draws from
the exercise templates. For checking that the meta-information is included correctly, it is often
helpful to run
exams_metainfo(exams2html("elasticity3.Rmd"))
Furthermore, some tweaking is usually required when calibrating the parameter ranges in the
data-generating process. The stresstest_exercise() function draws a large number of random replications
and thus can help to spot errors that occur or to find solutions that are “extreme” (e.g., much larger or smaller than usual). To clean up your
global environment and run the function use something like this:
rm(list = ls())
s <- stresstest_exercise("elasticity3.Rmd", n = 200)
plot(s)
plot(s, type = "solution")
The latter command plots the correct solution against the (scalar) parameters that were
generated in the exercise. This might show patterns for which parameters the solution becomes
too large or too small etc. See ?stresstest_exercise for further features/details.
Dynamic single-choice
To go from the dynamic numeric exercise to a dynamic single-choice exercise we need to
extend the data-generating process to also produce a number of wrong alternatives.
The function num_to_schoice() helps with this by providing different sampling
mechanisms. It allows to set a range in which the alternatives have to be, a minimum
distance between all alternatives, possibly include typical wrong solutions, etc.
It also shuffles the resulting alternatives and tries to make sure that the correct
solution is not a certain order statistic (e.g., almost always the largest or
smallest alternative).
The R/exams templates
elasticity4.Rmd and
elasticity4.Rnw first
wrap the data-generating process into a while loop with while(sol > -0.11). This makes sure
that there is enough “space” for four wrong alternatives between -0.11 and 0, using a minimum
distance of 0.017. Subsequently, the four wrong alternatives are generated by:
## single-choice incl. typical errors err <- c(1/sol, sol/p, p/sol) err <- err[(err > -5) & (err < -0.2) & abs(err - sol) > 0.01] rng <- c(min(1.5 * sol, -1), -0.01) sc <- num_to_schoice(sol, wrong = err, range = rng, delta = 0.017, method = "delta", digits = 3)
This suggests a number of typical wrong solutions err (provided that they are not too small
or too large) and makes sure that the range rng is large enough. With these arguments
num_to_schoice() is run, see ?num_to_schoice for the details. The resulting sc list
contains suitable $questions and $solutions that can be easily embedded in an answerlist()
and in the meta-information. Sometimes it is useful to wrap num_to_schoice() into another
while() loop to make sure a valid result is found. See the deriv2
template for illustraion.
As before exams2html() and/or exams2pdf() can be used to display the random draws from
this exercise template. And some stress-testing could be carried out by:
rm(list = ls())
s <- stresstest_exercise("elasticity4.Rmd", n = 200)
plot(s)
plot(s, type = "ordering")
As a final variation we could include None of the above as the last alternative. This is very easy because we can simply replace the fifth element of the question list with the corresponding string:
sc$questions[5] <- "None of the above."
No matter whether this was actually the correct alternative or one of the incorrect alternatives, the corresponding solution will stay the same. The R/exams templates elasticity5.Rmd and elasticity5.Rnw incorporate this additional line of code in the data-generating process.